Runkolukusarjamallit ovat aikansa lapsia – onko eri-ikäisrakenteisiin metsiin soveltuvia parametrisia malleja tai menetelmiä?
Siipilehto J. (2022). Runkolukusarjamallit ovat aikansa lapsia – onko eri-ikäisrakenteisiin metsiin soveltuvia parametrisia malleja tai menetelmiä? Metsätieteen aikakauskirja vuosikerta 2022 artikkeli 10703. https://doi.org/10.14214/ma.10703
Tiivistelmä
Metsätaloudessa on viime aikoina esiintynyt kasvavaa painetta metsien jatkuvan kasvatuksen vaihtoehtoon niin luonnon monimuotoisuuden, maiseman kuin hiilensidonnankin kannalta. Poimintahakkuisiin perustuvassa eri-ikäismetsätaloudessa optimaalinen runkolukusarja on laskeva. Tällaiset puuston rakenteet ovat käytännössä harvinaisia, koska metsätalous on viimeisten vuosikymmenien aikana suurelta osin perustunut alaharvennettujen tasaikäisrakenteisten metsien kasvatukseen. Tässä työssä tarkasteltiin Suomessa laadittuja läpimittajakaumamalleja alkaen ensimmäisestä, vuonna 1980 laaditusta Beta-jakaumamallista vuonna 2013 esiteltyyn Weibull-jakauman parametrien palautusmenetelmään. Tarkastelluista SB-jakaumamalleista yksi vaihtoehto oli laadittu Virossa. Kiinnostuksen kohteena oli, löytyykö kyseisistä parametrisistä jakaumamalleista tai menetelmistä eri-ikäisrakenteisten metsien runkolukusarjaan sopivia vaihtoehtoja. Vanhimpien jakaumamallien tuottamat runkolukusarjat eivät juuri muuttuneet ennustettavan metsikön rakenteen muuttuessa eri-ikäisrakenteisesta metsästä tasaikäisrakanteiseen viljelymetsään. SB-jakauman ennustemallit olivat kaikkein herkimpiä lähtöpuuston rakenteen muutoksille. Kuitenkin parametrien palautusmenetelmät olivat ennustemalleja luotettavampia, ja palautettu Weibull-jakauma oli yhteensopivin niin eri-ikäisrakenteisen kuin viljelykuusikonkin runkolukusarjojen kanssa.
Avainsanat
jakaumamallit;
läpimittajakaumat;
puuston rakenne
Vastaanotettu 21.1.2022 Hyväksytty 14.4.2022 Julkaistu 12.5.2022
Katselukerrat 36359
Saatavilla https://doi.org/10.14214/ma.10703 | Lataa PDF

1 Johdanto
Läpimittajakaumamalleja on laadittu oman aikansa metsätalouden suunnittelujärjestelmien tueksi. Kun metsäsuunnittelua tehtiin MTS/Alue- ja TASO-suunnittelujärjestelmien aikaan 1970- ja 1980-luvuilla, niin varttuneen puuston määrää kuvattiin pohjapinta-alana (G) ja koko puuston yhteisillä keskitunnuksilla, pohjapinta-alan mediaanipuun läpimitan (DGM) ja pituuden (HGM) avulla. Puulajisuhteet kuvattiin osuuksina pohjapinta-alasta tai tilavuudesta. Valtakunnan metsien inventoinnin (VMI) puuston kuvaus vastasi tätä aina vuosina 1996–2003 tehtyyn yhdeksänteen inventointiin (VMI9) saakka. Kun TASO-suunnittelujärjestelmästä siirryttiin 1990-luvulla SOLMU-suunnittelujärjestelmään, metsikön puulajiositteet pyrittiin kuvaamaan tarkemmin (Paananen 2002). Kullakin puulajiositteella oli omat tunnukset: G, DGM ja HGM tai taimikoissa runkoluku (N), aritmeettinen keskiläpimitta (D) ja keskipituus (H). Vuosina 2004–2008 mitattu VMI10 ja sitä tuoreemmat inventoinnit kuvaavat puuston SOLMU-muotoisella ositekohtaisella kuviotiedolla, mutta taimikoissa arvioitiin runkoluvun lisäksi vain taimien keskipituus. Vuodesta 2010 lähtien on yksityismetsien metsäsuunnittelu perustunut yhä enemmän laserkeilausinventointeihin. Kun SOLMU-aikakauden jälkeen metsäsuunnittelussa siirryttiin soveltamaan laserkeilauksen mittaustietoa (airborne laser scanning, ALS), on sen tulkintana siitä lähtien saatu arviot männyn (Pinus sylvestris L.), kuusen (Picea abies (L.) H. Karst.) ja lehtipuuston keski- ja summatunnuksista. ALS-aikakauden summatunnuksia ovat pohjapinta-alan ja runkoluvun lisäksi puuston tilavuus (V) ja keskitunnuksina pohjapinta-alapainotteinen keskiläpimitta (DG) ja pohjapinta-alapainotteinen pituus (HG). VMI:n maastoaineiston keruuseen ei ole toistaiseksi lisätty runkolukua varttuneiden puustojen kuviotietoihin. Sen sijaan VMI12:sta lähtien puumittaukset tehdään kiinteäsäteisiltä koealoilta, joilta saadaan luotettavat puustotunnukset ja erityisesti relaskooppikoealoja luotettavampi runkoluku.
Läpimittajakauma (runkolukusarja) on ennustettu kunakin aikakautena edellä esitettyjen puustoa kuvaavien tunnusten perusteella. Kuitenkin ns. SOLMU-aikakaudella jakaumatutkimuksissa tuotiin esiin, että runkoluku lisätietona mahdollistaisi varttuneen puuston runkolukusarjojen vaihtelun kuvauksen (Siipilehto 1999; Kangas ja Maltamo 2000b). Toisin sanoen, jos kiinnitetään puuston pohjapinta-ala ja keskiläpimitta tiettyyn arvoon, voidaan runkoluvun vaihtelulla saada aikaan hyvin erilaisia jakaumia: laskevia, oikealle tai vasemmalle vinoja tai symmetrisiä. Puuston pohjapinta-ala, keskiläpimitta ja -pituus määrittävät melko tarkasti puuston kokonaistilavuuden. Siten kokonaistilavuus vaihtelee vain vähän runkolukuvaihtelun mukaan, mutta puutavaralajien osuuksiin tulee merkittäviä eroja (Ahtikoski ym. 2018).
Jakaumafunktioissa on suuria eroja siinä, minkälaisia jakauman muotoja ne pystyvät kuvaamaan (Hafley ja Schreuder 1977). Weibull-jakauman joustavuus riittää kuvaamaan symmetrisyyden lisäksi jakauman molemminpuolista vinoutta. Johnsonin SB- ja Beta-jakaumat ovat joustavampia ja ne voivat kuvata molemminpuolisen vinouden lisäksi U-muotoista kaksihuippuisuutta, jossa huiput ovat jakauman ääripäissä. Gamma-jakauma on aina oikealle vino (jakauman pitkä häntä osoittaa oikealle). Normaali-, eksponentti- ja tasajakaumalla on vain yksi muoto.
Tyypillisesti läpimittajakaumat sovitetaan puutason mittausaineistoihin suurimman uskottavuuden menetelmällä hyödyntäen koko mitattua puujoukkoa. Estimoiduille jakaumaparametreille laaditaan ennustemalli puustotunnusten avulla. Menetelmä ei ole maailmalla suuressa suosiossa, koska puustotunnusten ja jakaumaparametrien riippuvuutta pidetään varsin heikkona (Bowling ym. 1989). Tästä syystä ei voi lähtökohtaisesti sanoa, että muodoltaan joustavin jakauma olisi myös paras jakauma ennustettavaksi. Joustavissa jakaumissa on kolme tai neljä parametria ja riippuvuus puuston kehitysvaiheesta voi olla vaikeasti hahmotettavissa. Momentti- ja prosenttiosuusmenetelmiä on käytetty maailmalla melko varhain metsäalan sovelluksissa (Bailey ja Dell 1973; Mønness 1982; Burk ja Newberry 1984). Nimensä mukaisesti näissä menetelmissä jakaumaennusteiden tuottamiseen riittää yksittäisten puiden sijaan jakauman momentit tai prosenttiosuuspisteet (fraktiilit), joita tulee tuntea yhtä monta kuin jakaumafunktiossa on parametreja. Siten 2-parametrisen Weibull-jakauman ratkaisemiseksi riittää ensimmäinen ja toinen momentti tai kaksi prosenttiosuuspistettä. Palautusmenetelmissä ennustetaan momentteja ja/tai prosenttiosuuksia jakauman parametrien sijaan.
Suomessa ennustemalleja alettiin laatia ns. kokopuuston pohjapinta-alan läpimittajakaumina 1980-luvulla perustuen Beta-jakaumaan (Päivinen 1980). Siipilehto (1988) laati vastaavat mallit Beta-jakaumalle kuin Päivinen (1980) ja myöhemmin Maltamo ym. (1995) vertasi Beta- ja Weibull- jakaumia keskenään. Ensimmäisiä puulajikohtaisia pohjapinta-alan läpimittajakaumien ennusteita laativat Mykkänen (1986) männylle ja Kilkki ym. (1989) kuuselle ja myöhemmin myös Maltamo (1997). Siipilehto (1999) testasi runkolukua lisämuuttujana SB- ja Weibull-jakaumien ennustamiseksi. Ensimmäisessä Beta-jakaumamallissa aineistona oli 1950-luvulla kerätty VMI3-aineisto (Päivinen 1980). Vanhimmissa Weibull-jakaumamalleissa käytettiin 1980-luvun vaihteessa mitattuja VMI7:n koepuukoealoja, joilla oli keskimäärin vain kahdeksan puuta metsikköä kohti (Kilkki ym. 1989). Tultaessa 1990-luvulle Beta- ja Weibull-jakaumamalleja laadittiin Itä- ja Keski-Suomeen painottuvasta metsäyhtiön metsien aineistosta, jossa puiden lukumäärä metsikköä kohti oli keskimäärin yli 70 (Maltamo ym. 1995; Maltamo 1997). Siipilehdon (1999) malleissa aineistona oli subjektiivisesti valittuja mänty–koivu- ja kuusi–koivusekametsiköitä, joissa kultakin koealalta mitattujen puiden määrä oli noin 120.
2000-luvulla jakaumatutkimukset keskittyivät erilaisiin tilastollisiin menetelmiin: prosenttiosuusmallit, regressioestimoinnin vaihtoehtoiset tekniikat, lineaarinen ennustaminen (BLUP) puustotunnusten sekä jakaumaparametrien lokalisoimiseksi, jakauman kalibrointiestimointi ja parametrien palautusmenetelmä. Prosenttiosuusmalleissa ennustetut prosenttipisteet yhdistetään kernel-tasoituksella (Kangas ja Maltamo 2000b), jolloin jakauman muoto voi olla hyvin vaihteleva. Siipilehto ym. (2007) todistivat, että rämepuustojen jakaumia ennustettaessa kehittyneillä regressiotekniikoilla saatiin perinteisiä malleja luotettavampia ennusteita. BLUP-menetelmän etu on joustavuus, koska mitä tahansa tunnettua malliperheen puustotunnusta voidaan käyttää parametrien lokalisointiin. Laaditun malliperheen kahdeksan puustotunnuksen matriisi pitää sisällään 255 erilaista lineaarista ennustemallia jakaumaparametreille (Siipilehto 2011). Uusissa tutkimuksissa tuotiin esiin, että jakaumaa ennustettaessa kahden selittävän summatunnuksen (G ja N) tai keskitunnuksen (esim. DGM ja mediaani-DM) avulla saadaan läpimittajakauman muodon vaihtelu kuvattua paremmin (Kangas ja Maltamo 2000b; Maltamo ym. 2000; Siipilehto ym. 2007). Koska parametrien ennustemalleilla ei kuitenkaan päästä täydelliseen selittäviä muuttujia vastaavaan kuvaukseen, on ennustettuja jakaumia kalibroitu. Kalibrointiestimoinnissa jakauman muotoa korjataan mahdollisimman tehokkaasti siten, että jakauma toteuttaa lähtötietoina annetut keski- ja summatunnukset (Kangas ja Maltamo 2000a). Parametrien palautusmenetelmällä ratkaistu jakaumafunktio tuottaa aidosti lähtötietojen puustotunnukset (G, N ja keskitunnus). Tyypillisesti palautusmenetelmä esitellään momenttimenetelmänä, jolloin keskitunnus on aritmeettinen keskiarvo (D) eli ensimmäinen momentti ja pohjapinta-alasta ja runkoluvusta saadaan toinen momentti kaavalla G/(N × π/2002). Siipilehto ja Mehtätalo (2013) esittelivät palautusyhtälöt D:n lisäksi myös mediaaneille DM ja DGM sekä painotetulle keskiarvolle DG.
Ruotsissa ja Norjassa läpimittajakaumien mallitus on ollut keskenään samankaltaista, mutta erilaista kuin Suomessa. Johnsonin SB-jakaumaa käytettiin jo 1980-luvulla, ja jakaumat palautettiin fraktiilien avulla parametrien ennustamisen sijaan. Malleja laadittiin tasaikäisrakenteisille metsiköille: Mønness (1982) männylle, Tham (1988) nuorille kuusi–koivusekametsille ja Holte (1993) kuusikoille. Holte (1993) tarkasteli SB-jakauman lisäksi Weibull-jakaumaa. Virossa on tehty 2000-luvulla SB-jakaumamalleja, joissa ennusteet laadittiin läpimittajakauman ala- ja ylärajalle sekä hajonnalle (Kiviste ym. 2003). Näiden ennusteiden avulla jakauman muotoparametrit palautettiin momenttimenetelmällä.
Metsätaloudessa on viime aikoina esiintynyt kasvavaa painetta jatkuvan kasvatuksen vaihtoehtoon niin monimuotoisuuden, maiseman kuin hiilensidonnankin kannalta. VMI12-maastotyöstä lähtien puuston jaksoisuustunnus sisältää koodin, jolla tarkoitetaan metsikön olevan eri-ikäisrakenteinen. Koska eri-ikäisrakenteisen metsän runkolukusarja on laskeva tai hyvin vino, tiettyä keskiläpimittaa ja pohjapinta-alaa vastaava runkoluku on huomattavasti suurempi kuin tasaikäisrakenteisessa metsässä. Tällaiset puuston rakenteet ovat käytännössä harvinaisia, koska metsätalous on viimeisten vuosikymmenien aikana suurelta osin perustunut alaharvennettujen tasaikäisrakenteisten metsien kasvatukseen. Silti on syytä tarkastella, onko meillä olemassa jakaumamalleja tai menetelmiä tällaisten eri-ikäisrakenteisten metsien runkolukusarjojen ennustamiseksi. Tässä työssä tarkasteltiin parametristen jakaumien ennustemallien ja palautusmenetelmien sopivuutta erilaisten runkolukusarjojen ennustamiseksi.
2 Aineisto ja menetelmät
2.1 Metsiköt jakaumien testaukseen
Parhaiten läpimittajakaumamallien ominaisuudet tulevat esiin, kun vaihtoehtoisia malleja tarkastellaan runkolukusarjaltaan täysin erilaisten metsiköiden avulla. Jakaumaennusteita verrattiin eri-ikäisrakenteisen koealan (ERIKA) ja viljellyn kuusikon harvennuskokeen koealan (HARKAS) havaittuihin runkolukusarjoihin. Lisäksi puulajeittain laadittuja malleja tarkasteltiin luontaisesti syntyneen kuusi–koivusekametsän (KUKO) avulla. Puuston tiheys vaihteli eri-ikäisrakenteisen metsikön 2195 ha–1 runkoluvusta sekametsän runkolukuun 1680 ha–1 ja harvennetun viljelymetsikön runkolukuun 725 ha–1. Luontaisen KUKO-sekametsän kokonaispohjapinta-ala oli 30 m2 ha–1, josta kuusen osuus oli 16 m2 ha–1. ERIKA-koealoilla vastaavat pohjapinta-alat olivat 22,4 m2 ha–1 ja 17 m2 ha–1 ja HARKAS-koealalla oli pelkästään kuusta 21 m2 ha–1. Aritmeettiset keskiläpimitat erosivat huomattavasti pieniläpimittaisen puuston osuuden mukaan ja olivat ERIKA-koealalla 9 cm, KUKO-koealalla 14 cm ja HARKAS-koealalla 19 cm, kun samanaikaisesti DGM oli näillä koealoilla lähes sama: 19, 18 ja 19 cm.
2.2 Jakaumamallit ja niiden validointi
Tarkasteltavat Beta-jakauman kokopuuston ennustemallit olivat: B_1980 (Päivinen 1980), B_1988 (Siipilehto 1988) ja B_1995 (Maltamo ym. 1995). Weibull-jakauman ennustemalleista osa oli kahden parametrin (W2) ja osa kolmen parametrin (W3) malleja. Tarkasteltavana olivat: W3_1989 (Kilkki ym. 1989), W2_1995 ja W3_1995 (Maltamo ym. 1995) kokopuustolle sekä puulajikohtaiset W3_1997 (Maltamo 1997) ja W2_1999 (G) ilman runkolukutietoa (Siipilehto 1999) että palautusmenetelmä W2_2013 (Siipilehto ja Mehtätalo 2013). Weibull-jakauman parametrien palautukseen valittiin keskitunnukseksi DGM, koska se oli yleisin selittäjä jakaumamalleissa. Tarkasteltavia SB-jakaumien ennustemalleja olivat kolmen parametrin (alaraja = 0) SB3_1999 (G + N), jossa runkoluku on mukana (Siipilehto 1999) ja rämemänniköille laadittu SB3_2007 (Siipilehto ym. 2007) sekä virolainen palautusmenetelmä neljälle parametrille SB4_2003 (Kiviste ym. 2003). KUKO-sekametsässä kuusen ja koivun (Betula spp. L.) runkolukusarjat olivat keskenään erimuotoisia. Yhteinen kokopuuston runkolukusarja oli lievästi kaksihuippuinen. KUKO-metsikölle jakaumamalleja testattiin kokopuuston jakaumina ja lisäksi puulajeittain, kun mallit oli laadittu puulajiositteille. Parametrin palautusmenetelmä W2_2013 sopii kumpaankin vaihtoehtoon. Koska ennustemallit oli laadittu pohjapinta-alan läpimittajakaumina ja jakauma skaalattiin pohjapinta-alaan, virheet laskettiin runkoluvun suhteen. Poikkeuksena frekvenssijakaumamalli SB4_2003, jonka yhteydessä laskettiin pohjapinta-alan suhteellinen virhe. Summatunnuksen virheen lisäksi jakaumien yhteensopivuutta havaintoaineistoihin tarkasteltiin visuaalisesti ja Kolmogorovin-Smirnovin yhteensopivuustestin avulla.
3 Tulokset
3.1 Jakauman tuottama virhe summatunnuksessa
ERIKA-metsikön runkoluku aliarvioitiin lukuun ottamatta W3_1995-mallia, joka tuotti 8 %:n yliarvion (Taulukko 1). Yleisesti runkoluvun aliarviot olivat ERIKA-metsikössä varsin huomattavia (24–62 %), mutta W2_1995 tuotti maltillisen 11 %:n aliarvion. Vastaavasti mallit yliarvioivat systemaattisesti viljellyn HARKAS-kuusikon runkoluvun, suurimmillaan kaksinkertaiseksi W3_1995-mallilla. Sen sijaan luontaisesti syntyneen KUKO-sekametsän kohdalla runkoluvun virheet olivat yleisesti pienempiä. Kuitenkin W3_1995-mallilla KUKO-sekametsän kokonaisrunkoluku yliarvioitui 34 %. SB-jakauman ennusteilla saatiin parhaimmillaan lähes virheettömiä runkolukuja ja vältettiin suurimmat virheet. Silti runkoluvun aliarviot ERIKA-kuusikossa olivat melko huomattavia, 24–26 % ja SB4_2003-frekvenssijakaumalla pohjapinta-alan virhe oli 16 %. Yleistäen voidaan sanoa, että selkeät runkoluvun aliarviot liittyvät ennustetun jakauman suppeuteen ja yliarviot liian leveään tai liiaksi oikealle vinoon jakaumaan.
| Taulukko 1. Runkoluvun suhteelliset virheet (havaittu – ennuste, %) vaihtoehtoisilla jakaumamalleilla. Paras mallin yhteensopivuus kussakin aineistossa on lihavoitu ja huonoin kursiivilla. | |||||||||
| Jakaumamalli | Jakauma-funktio | Ennustettava puusto | ERIKA | KUKO | HARKAS | ||||
| kuusi | kokopuusto | kuusi | koivu | kuusi | |||||
| B_1980 | Beta | koko | 55 | 8 | –35 | ||||
| B_1988 | Beta | koko | 50 | 5 | –34 | ||||
| B_1995 | Beta | koko | 33 | –19 | –78 | ||||
| W3_1989 | Weibull3 | koko | 62 | 27 | –16 | ||||
| W2_1995 | Weibull2 | koko | 11 | –22 | –83 | ||||
| W3_1995 | Weibull3 | koko | –8 | –34 | –103 | ||||
| W3_1997 | Weibull3 | osite | 40 | 13 | 22 | –13 | –25 | ||
| W2_1999 (G) | Weibull2 | osite | 55 | 8 | 23 | –8 | –40 | ||
| SB3_1999 (G + N) | SB | osite | 26 | –1 | –5 | –6 | –17 | ||
| SB3_2007 | SB | osite | 24 | 7 | 7 | –3 | –3 | ||
| SB4_2003* | SBN | osite | 16 | 9 | 14 | 5 | –1 | ||
| * = SB4_2003-frekvenssijakaumasta laskettu pohjapinta-alan virhe, %. | |||||||||
3.2 Jakauman visuaalinen yhteensopivuus
Vanhojen mallien jakaumaennusteilla oli varsin kiinteä muoto, joka ei mukautunut havaittuun runkolukusarjaan. Tällaisia olivat kaikki Beta-jakaumaennusteet, vaikka Beta-funktio itsessään on joustava. Beta-jakaumien vinous sopi paremmin ERIKA- kuin HARKAS-koealalle, mutta pieniläpimittainen puusto puuttui 3–7 cm:iin ennustetun minimiläpimitan vuoksi (Kuva 1, Beta). Tietyn Weibull-jakauman ennuste oli varsin samanmuotoinen runkolukusarjoiltaan erilaisissa ERIKA- ja HARKAS-metsiköissä, mutta ennustemallien välillä oli selkeitä eroja. W3_1989-mallilla Weibull-jakauman alarajaksi tuli 9 cm, kun taas W2_1995-malli tuotti suuren pieniläpimittaisen puuston osuuden 1 cm:n läpimittaluokkaan asti molemmissa metsiköissä (Kuva 1, Weibull). W3_1995-malli tuotti myös suuren pieniläpimittaisien puuston osuuden, mutta ERIKA-koealan kohdalla ennuste oli yksi parhaimmista (puuttui vain 1 cm:n läpimittaluokka). W3_1997-malli tuotti ennustetuista Weibull-jakaumista parhaan jakauman HARKAS-koealalle, mutta pieniläpimittaisen puuston osuus yliarvioitui. W2_1999 jakaumat olivat lähes saman muotoisia sekä ERIKA- että HARKAS-koealoilla eivätkä sopineet kumpaankaan havaittuun jakaumaan. Weibull-jakaumista vain parametrin palautusmenetelmä W2_2013 mukautui molempien esimerkkimetsiköiden runkolukusarjoihin. Ennustemalleista SB-jakaumissa oli eniten havaittujen runkolukusarjojen mukaista muodon vaihtelua. Silti mikään SB-jakaumaennuste ei pystynyt kuvaamaan ERIKA-metsikön runkolukusarjan vinoutta riittävästi, mutta HARKAS-viljelykuusikon runkolukusarjat sopivat yhteen havaitun runkolukusarjan kanssa (Kuva 1, SB).
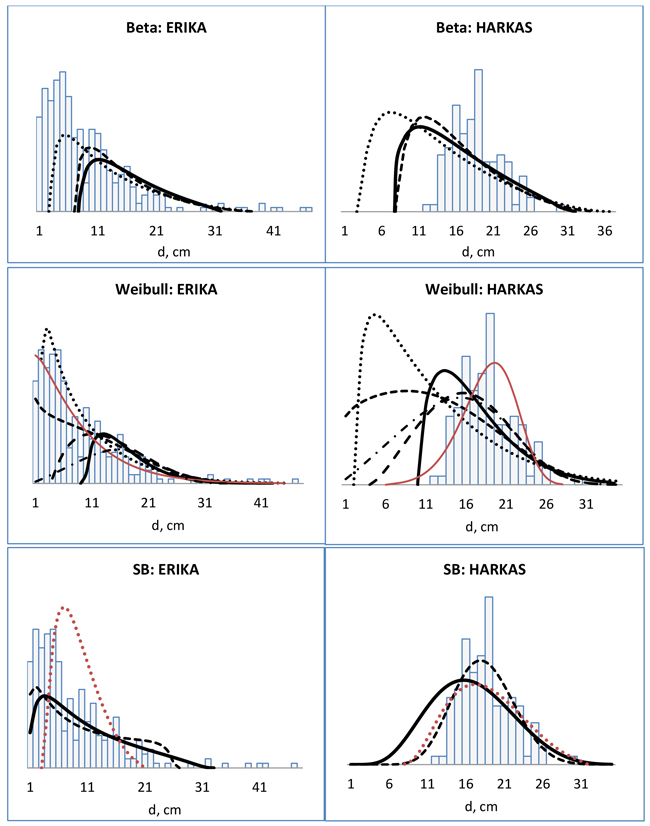
Kuva 1. Ennustetut runkolukusarjat eri-ikäisrakenteiselle (ERIKA) ja viljelykuusikolle (HARKAS). Mallien jakaumafunktiot olivat Beta: B_1980(—), B_1988 (- - -) ja B_1995 (···), Weibull: W3_1989 (—), W2_1995 (- - -) ja W3_1995 (···), W3_1997 (– – –), W2_1999 (– · –) ja W2_2013 (—) ja SB: SB3_1999 (—), SB3_2007 (- - -) ja SB4_2003 (···). Parametrien palautusmenetelmät punaisella .
KUKO-sekametsän runkolukusarjoja puulajeittain tarkasteltaessa Weibull-jakauman W3_1997 ennusteet olivat melko samanmuotoisia kuuselle ja koivulle, eivätkä ne vastanneet havaintoaineistoa (Kuva 2). W3_1997-malli ennusti kuusen jakauman symmetrisenä ja koivun jakauman voimakkaasti oikealle vinona, kun taas vastaavat havaitut jakaumat olivat oikealle ja vasemmalle vinoja. W2_1999-mallin ennuste kuuselle ei myöskään sopinut havaittuun jakaumaan, mutta koivun jakauma oli melko hyvin yhteensopiva. W2_2013-mallin palautetut jakaumat vastasivat hyvin havaittuja runkolukusarjoja. SB-jakauman vaihtoehdoissa kuusen osuudessa oli huomattavia eroja mallien välillä, mutta koivun jakaumat olivat keskenään lähes samanlaisia. SB4_2003-mallin palautettu jakauma kuuselle muistutti enemmän havaittua runkolukusarjaa kuin malllien SB3_1999 ja SB3_2007 ennusteet ja oli vinouden ja huipukkuuden suhteen parempi kuin W2_2013-mallin palautettu Weibull-jakauma.
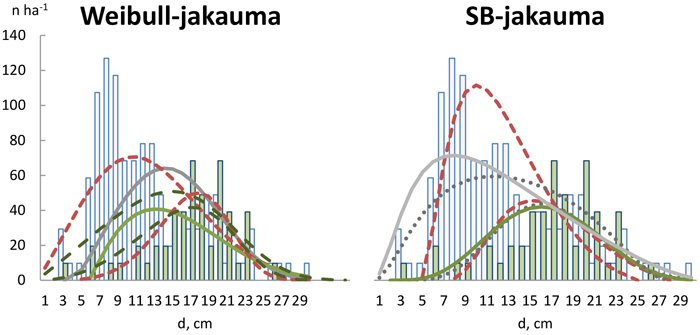
Kuva 2. Kuusen (harmaa) ja koivun (vihreä) runkolukusarjat Weibull- ja SB-jakaumilla ennustettuna. Weibull-jakaumat olivat W3_1997 (—) kolmen parametrin ja W2_1999 (– –) kahden parametrin pohjapinta-alan läpimittajakauma ja W2_2013 2-parametrisen frekvenssijakauman palautus (- - -). SB-jakaumat olivat SB3_1999 (—) ja SB3_2007 (···) pohjapinta-alan läpimittajakaumat sekä SB4_2003 (- - -) frekvenssijakauman palautus.
3.3 Jakauman tilastollinen yhteensopivuus
Kolmogorovin-Smirnovin yhteensopivuustestin mukaan mikään yksittäinen mallivaihtoehto ei ollut aina paras, mutta parametrien palautusmenetelmä tuotti jakaumaparametrien ennustamista parempia yhteensopivuuksia (Taulukko 2). Parametrien palautusmenetelmällä W2_2013-mallilla saatiin paras yhteensopivuus sekä eri-ikäisrakenteisessa että hoidetussa viljelymetsässä käyttämällä DGM-muuttujaa. Sen lisäksi palautus DG-muuttujan avulla tuotti parhaat yhteensopivuudet sekametsikön kokopuuston jakaumaksi ja sen koivuositteelle. Palautetulla SB-jakaumalla (SB4_2003) saatiin paras yhteensopivuus KUKO-sekametsän kuusiositteelle, vaikka pienimmät läpimittaluokat puuttuivat. Kyseisen sekametsän kokopuustoa ennustettaessa mallien SB3_1999 ja SB3_2007 SB-jakaumat sopivat jopa hieman paremmin havaintoaineistoon kuin Weibull-jakauman palautus DGM-muuttujalla. On myös syytä huomata, että puulajiositteille laaditut mallit olivat pääsääntöisesti tilastollisesti yhteensopivia eri metsiköiden havaintoaineistojen kanssa. Poikkeuksena olivat vain mallit W3_1997, W2_1999 ja SB4_2003 eri-ikäisrakenteiselle metsikölle ja W2_1999-malli viljelykuusikolle. Yksikään kokopuuston Beta- tai Weibull-jakauma ei ollut tilastollisesti yhteensopiva viljelykuusikon sinänsä selkeän runkolukusarjan kanssa.
| Taulukko 2. Kolmogorovin-Smirnovin testi suhdelukuna KSq = (supremus/kriittinen arvo), jolloin KSq < 1 merkitsee tilastollista yhteensopivuutta ja arvoilla KSq > 1 jakauma ei sovi aineistoon 10 %:n riskillä. Paras yhteensopivuus on lihavoitu ja huonoin kursiivilla. | |||||||||
| Jakaumamalli | Jakauma-funktio | Ennustettava puusto | ERIKA | KUKO | HARKAS | ||||
| kuusi | koko | kuusi | koivu | kuusi | |||||
| B_1980 | Beta | koko | 1,483 | 0,498 | 1,112 | ||||
| B_1988 | Beta | koko | 1,483 | 0,498 | 1,108 | ||||
| B_1995 | Beta | koko | 1,308 | 0,689 | 1,247 | ||||
| W3_1989 | Weibull3 | koko | 1,427 | 0,872 | 1,014 | ||||
| W2_1995 | Weibull2 | koko | 0,618 | 0,493 | 1,243 | ||||
| W3_1995 | Weibull3 | koko | 1,094 | 0,838 | 1,330 | ||||
| W3_1997 | Weibull3 | osite | 1,094 | 0,405 | 0,652 | 0,542 | 0,977 | ||
| W2_1999 (G) | Weibull2 | osite | 1,329 | 0,447 | 0,643 | 0,465 | 1,057 | ||
| W2_2013 (DGM) a | Weibull2N | osite | 0,337 | 0,400 | 0,466 | 0,343 | 0,504 | ||
| W2_2013 (DG) b | Weibull2N | osite | 0,493 | 0,362 | 0,470 | 0,326 | 0,827 | ||
| SB3_1999 (G + N) | SB | osite | 0,602 | 0,385 | 0,439 | 0,518 | 0,967 | ||
| SB3_2007 | SB | osite | 0,604 | 0,391 | 0,521 | 0,430 | 0,661 | ||
| SB4_2003 c | SBN | osite | 1,427 | 0,417 | 0,401 | 0,612 | 0,838 | ||
| a = parametrin palautuksessa käytetty keskitunnus oli DGM. b = parametrin palautuksessa käytetty keskitunnus oli DG. c = SB-jakauman palautusmenetelmä (Kiviste ym. 2003). | |||||||||
4 Tulosten tarkastelu ja johtopäätökset
Suomalaiset puuston läpimittajakaumamallit olivat pitkään voimakkaasti keskiarvoistavia pohjapinta-alan läpimittajakaumia. Tämä tarkoittaa sitä, että mallit pystyivät tuottamaan pohjapinta-alan (G) ja keskitunnuksen (DGM) avulla vain yhden muotoisia jakaumia tai joillakin lisätunnuksilla marginaalista vaihtelua odotusarvojakauman ympärille. Osa vanhojen jakaumamallien ennusteista sopi paremmin eri-ikäisrakenteisen metsikön kuin tasaikäisrakenteisen viljelykuusikon kuvaukseen. Ennustettujen Beta-jakaumien muoto oli muuten ERIKA-havaintoaineiston mukainen, mutta pieniläpimittaisin puusto puuttui ennustetun puuston 3–8 cm:n minimiläpimitan vuoksi. Koska Beta- ja Weibull-jakaumien ennustemalleissa selittäjinä oli G- ja DGM-muuttujien lisäksi yleensä ikä ja toisinaan keskipituus, niin pientä vaihtelua pohjapinta-alan ja keskiläpimitan määrittämään läpimittajakaumaan tuli iän ja keskipituuden vaihteluista. Weibull-jakaumista W3_1995-malli sopi erinomaisesti eri-ikäisrakenteisen metsikön runkolukusarjaan 1 cm:n läpimittaluokkaa lukuun ottamatta. Valitettavasti ennustetun W3_1995-jakauman muoto säilyi lähes muuttumattomana, kun lähtöpuuston tiedot poimittiin viljelykuusikosta. Vaikka joustavan SB-jakauman ennustemallit sopivat yleensä melko hyvin havaintoaineistoihin, niin SB4_2003-mallin palautettu jakauma ei kuitenkaan sopinut eri-ikäisrakenteisen metsikön laskevaan runkolukusarjaan, koska myös tässä vaihtoehdossa ennustettu minimiläpimitta leikkasi alle 4 cm:n puuston pois. Tarkasteltaessa kuusi–koivusekametsikön runkolukusarjoja puulajeittain huomataan, että ne ovat keskenään erimuotoisia – kuusi oikealle vino ja koivu vasemmalle vino. Palautetulla Weibull-jakaumalla koivun runkolukusarja oli visuaalisesti yhteensopiva. Jos vanhoista kokopuuston jakaumista erotettaisiin kuusi- ja koivuositteet puulajin osuutena pohjapinta-alasta kuten TASO-suunnittelujärjestelmän aikana tehtiin, niin runkolukusarjat saisivat virheellisen muodon.
Viljelykuusikoissa vanhoilla jakaumamalleilla saadut suuret runkoluvun yliarviot johtuivat siitä, että laadinta-aineistoissa ei juuri ole ollut viljelymetsiä ja luontaisissa kuusikoissa pieniläpimittaisten kuusten suhteellinen osuus on suurempi kuin viljelymetsissä. Erityisesti on huomattava, että B_1980-mallin laadinnassa käytetty VMI3-aineisto on kerätty 1950-luvulla, jolloin varttuneita viljelymetsiä ei ole voinut osua otokseen. Toisaalta Siipilehdon (1999) SB- ja Weibull-jakaumamalleissa aineistona oli pelkästään luontaisesti syntyneitä sekametsiä ja Siipilehdon ym. (2007) SB3_2007-malli on laadittu ojitettujen rämeiden aineistosta, jossa ei myöskään ollut istutusmetsiä. Kuitenkin rämepuustojen runkolukusarjojen monipuolisuus oli suuri etu jakaumamallinnuksessa, ja laadittua mallia voitiin soveltaa eri puulajeille sekä kivennäis- että turvemailla. Korpikuusikoissa olisi voinut olla vielä enemmän vaihtelua runkolukusarjoissa (Sarkkola ym. 2003).
Tarkastelluista vaihtoehdoista Weibull-jakauman palautus oli ylivoimainen menetelmä niin viljelymetsässä kuin eri-ikäisrakenteisessa metsikössäkin. Parametrin palautuksessa käytettiin aluksi DGM-muuttujaa, joka on tyypillisesti ollut selittävänä muuttujana suomalaisissa jakaumamalleissa. Viime aikoina on huomattu, että parametrien palautuksessa keskiläpimitta D on selvästi parempi tunnus kuin mediaani DM ja että DG on taimivaihetta lukuun ottamatta paras keskitunnus (Lee ym. 2021). Siksi jakaumien yhteensopivuustestit laskettiin myös DG-vaihtoehdoille. Tarkastelluissa esimerkkitapauksissa kummatkin keskitunnukset tuottivat kahdesti parhaan jakaumasovituksen.
Tulosten perusteella on selvää, että parametrisia jakaumia sovellettaessa tulee siirtyä parametrien ennustamisesta parametrien palautusmenetelmiin. Lisäksi jatkossa parametrien palautus tulisi tehdä katkaistuna jakaumana, jos havaintoaineiston keruu on rajattu tiettyyn minimiläpimittaan (Merganič ja Sterba 2006), kuten VMI12 kiinteäsäteisillä koealoilla, joilla lukupuiden pienin läpimitta on 4,5 cm. Katkaistuna jakaumana sovitettaessa ennusteista saadaan entistä tarkempia silloin, kun jakauma sisältää pieniläpimittaista puustoa, ja samalla vältetään konvergoitumisongelmia. Nykyisen ALS-tulkinnan puustotunnukset tukevat palautusmenetelmän käyttöä ja hilaruuduille palautetuista Weibull-jakaumista on saatu hyviä kokemuksia (Siipilehto ym. 2016). Kun on tehty vertailuja eri menetelmien välillä (perinteinen maastoinventointi vs. ALS), tutkimuksissa käytetyt jakaumamallit ovat olleet vanhoja, keskiarvoistavia malleja (esim. Holopainen ym. 2010). Jatkossa, jos ALS-aineistojen yhteydessä halutaan vertailla ei-parametrisia ja parametrisia menetelmiä keskenään, tulisi parametriseksi verrokkimenetelmäksi valita paras vaihtoehto (ks. Maltamo ym. 2018) eikä missään tapauksessa vanhoja keskiarvoistavia jakaumamalleja. Tulevaisuudessa tiheäpulssisen laserpisteaineiston yhteydessä aluepohjaisen tulkinnan rinnalle tulee yksinpuintulkinta, jossa jakaumamalleja ei tarvita tai niitä hyödynnetään piiloon jäävän pieniläpimittaisen puuston täydentämiseksi (Holopainen 2019).
Lähteitä
Ahtikoski A, Siipilehto J, Salminen H, Lehtonen M, Hynynen J (2018) Effect of stand structure and number of sample trees on optimal management for Scots pine: a model-based study. Forests 9, article id 750. https://doi.org/10.3390/f9120750.
Bailey RL, Dell TR (1973) Quantifying diameter distributions with the Weibull function. For Sci 19: 97–104. https://doi.org/10.1093/forestscience/19.2.97.
Bowling EH, Burkhart HE, Burk TE, Beck DE (1989) A stand-level multispecies growth model for Appalachian hardwoods. Can J Forest Res 19: 405–412. https://doi.org/10.1139/x89-064.
Burk TJ, Newberry JD (1984) A simple algorithm for moment-based recovery of Weibull distribution parameters. For Sci 30: 329–332. https://doi.org/10.1093/forestscience/30.2.329.
Hafley WL, Schreuder HT (1977) Statistical distributions for fitting diameter and height data in even-aged stands. Can J Forest Res 7: 481–487. https://doi.org/10.1139/x77-062.
Holopainen M (2019) Metsien kaukokartoitus – digitalisaatiota, täsmämetsätaloutta ja 4D-geoinformatiikkaa. Metsätieteen aikakauskirja, artikkelitunnus 10214. https://doi.org/10.14214/ma.10214.
Holopainen M, Vastaranta M, Rasinmäki J, Kalliovirta J, Mäkinen A, Haapanen R, Melkas T, Yu X, Hyyppä J (2010) Uncertainty in timber assortment estimates predicted from forest inventory data. Eur J Forest Res 129: 1131–1142. https://doi.org/10.1007/s10342-010-0401-4.
Holte A (1993) Diameter distribution functions for even-aged (Picea abies) stands. Research Paper of Skogforsk 46: 1–47.
Kangas A, Maltamo M (2000a) Calibrating predicted diameter distribution with additional information. For Sci 46: 390–396. https://doi.org/10.1093/forestscience/46.3.390.
Kangas A, Maltamo M (2000b) Percentile based basal area diameter distribution models for Scots pine, Norway spruce and birch species. Silva Fenn 34: 371–380. https://doi.org/10.14214/sf.619.
Kilkki P, Maltamo M, Mykkänen R, Päivinen R (1989) Use of the Weibull function in the estimation the basal area dbh-distribution. Silva Fenn 23: 311–318. https://doi.org/10.14214/sf.a15550.
Kiviste A, Nilso A, Hordo M, Merenäkk M (2003) Diameter distribution models and height-diameter equations for Estonian forests. Julkaisussa: Amaro A, Reed D, Soares P (toim) Modelling forest systems. CAB International. ISBN 0 85199 693 0.
Lee D, Siipilehto J, Hynynen J (2021) Models for diameter distribution and tree height in hybrid aspen plantations in southern Finland. Silva Fenn 55, article id 10612. https://doi.org/10.14214/sf.10612.
Maltamo M (1997) Comparing basal area diameter distributions estimated by tree species and for the entire growing stock in a mixed stand. Silva Fenn 31: 53–65. https://doi.org/10.14214/sf.a8510.
Maltamo M, Puumalainen J, Päivinen R (1995) Comparison of beta and Weibull functions for modelling basal area diameter distribution in stands of Pinus sylvestris and Picea abies. Scand J Forest Res 10: 284–295. https://doi.org/10.1080/02827589509382895.
Maltamo M, Kangas A, Uutera J, Torniainen T, Saramäki J (2000) Comparison of percentile based prediction methods and the Weibull distribution in describing the diameter distribution of heterogeneous Scots pine stands. Forest Ecol Manag 133: 263–274. https://doi.org/10.1016/S0378-1127(99)00239-X.
Maltamo M, Mehtätalo L, Vauhkonen J, Packalén P (2018). Airborne laser scanning for tree diameter distribution modelling: a comparison of different modelling alternatives in a tropical single-species plantation. Forestry 91: 121–131. https://doi.org/10.1093/forestry/cpx041.
Merganič J, Sterba H (2006) Characterisation of diameter distribution using the Weibull function: method of moments. Eur J Forest Res 125: 427–439. https://doi.org/10.1007/s10342-006-0138-2.
Mønness EN (1982) Diameter distributions and height curves in even- aged stands of Pinus sylvestris L. Medd Norsk I Skogfor 36: 1–43.
Mykkänen R (1986) Weibull-funktion käyttö puuston läpimittajakauman estimoinnissa. Metsätalouden syventävien opintojen tutkielma, Joensuun yliopisto.
Paananen R (2002) Uuden metsäsuunnittelujärjestelmän kehittämisen lähtökohtia ja tavoitteita. Metsätieteen aikakauskirja 3/2002: 532–536. https://doi.org/10.14214/ma.6190.
Päivinen R (1980) Puiden läpimittajakauman estimointi ja siihen perustuva puustotunnusten laskentamenetelmä. Folia Forestalia 442. http://urn.fi/URN:ISBN:951-40-0461-2.
Sarkkola S, Alenius V, Hökkä H, Laiho R, Penttilä T, Päivänen J (2003) Changes in structural inequality in Norway spruce stands after water-level drawdown. Can J Forest Res 33: 222–231. https://doi.org/10.1139/x02-179.
Siipilehto J (1988) Metsätalouskuvioiden läpimittajakaumien ennustaminen beta-funktiolla. Pro gradu -työ. Helsingin yliopisto, metsänarvioimistieteen laitos.
Siipilehto J (1999) Improving the accuracy of predicted basal-area diameter distribution in advanced stands by determining stem number. Silva Fenn 33: 281–301. https://doi.org/10.14214/sf.650.
Siipilehto J (2011) Methods and applications for improving parameter prediction models for stand structures in Finland. Diss For 124. https://doi.org/10.14214/df.124.
Siipilehto J, Mehtätalo L (2013) Parameter recovery vs. parameter prediction for the Weibull distribution validated for Scots pine stands in Finland. Silva Fenn 47, article id 1057. https://doi.org/10.14214/sf.1057.
Siipilehto J, Sarkkola S, Mehtätalo L (2007) Comparing regression estimation techniques when predicting diameter distributions of Scots pine on drained peatlands. Silva Fenn 41: 333–349. https://doi.org/10.14214/sf.300.
Siipilehto J, Lindeman H, Vastaranta M, Yu X, Uusitalo J (2016) Reliability of the predicted stand structure for clear-cut stands using optional methods: airborne laser scanning-based methods, smartphone-based forest inventory application Trestima and pre-harvest measurement tool EMO. Silva Fenn 50, article id 1568. https://doi.org/10.14214/sf.1568.
Tham Å (1988) Structure of Mixed Picea abies (L.) Karst. and Betula pendula Roth and Betula pubescens Ehrh. Stands in South and Middle Sweden. Scand J Forest Res 3: 355−369. https://doi.org/10.1080/02827588809382523.
30 viitettä.