Ikä vaikuttaa kuusen kuolleisuuteen
Siipilehto J., Mäkinen H., Peltoniemi M. (2021). Ikä vaikuttaa kuusen kuolleisuuteen. Metsätieteen aikakauskirja vuosikerta 2021 artikkeli 10576. https://doi.org/10.14214/ma.10576
Vastaanotettu 31.5.2021 Hyväksytty 6.6.2021 Julkaistu 8.6.2021
Katselukerrat 7240
Saatavilla https://doi.org/10.14214/ma.10576 | Lataa PDF

Seloste artikkelista Siipilehto J., Mäkinen H., Andreassen K., Peltoniemi M. (2021). Models for integrating and identifying the effect of senescence on individual tree survival probability for Norway spruce. Silva Fennica vol. 55 no. 2 article id 10496. https://doi.org/10.14214/sf.10496.
Ikääntyminen ja kilpailu heikentävät puiden veden ja ravinteiden saantia, joka altistaa ne kuolemiselle. Joissakin tutkimuksissa kuusen eloonjäämisen on havaittu laskevan suurissa läpimittaluokissa, mutta iän vaikutusta ei ole otettu huomioon. Tässä tutkimuksessa tarkasteltiin kuusen ikääntymisen vaikutusta eloonjäämiseen sovittamalla useita vaihtoehtoisia eloonjäämismalleja. Mallit sovitettiin aineistoon, joka koostui suomalaisista käsitellyistä ja käsittelemättömistä kuusen kestokoealoista (HARKAS), kuusivaltaisista luonnonmetsistä ja norjalaisista kuusen kestokoealoista, joista osa oli harvennettu perustamisen yhteydessä. Metsiköiden valtapuuston keski-iän vaihtelualue oli HARKAS-aineistossa 27–88 vuotta, norjalaisessa aineistossa 19–148 vuotta ja luonnonmetsissä 100–290 vuotta.
Mallit laadittiin logistisella regressiolla. Eloonjäämismallin yleinen muoto oli:
![]()
jossa P on eloonjäämisen todennäköisyys mittausjakson aikana, X'b lineaarinen malli selittävistä muuttujista X ja niille estimoiduista parametreista b. Eksponentin t avulla huomioitiin erimittaisten mittausjaksojen vaikutus. Mallit estimoitiin sekamalleina binääriselle vastemuuttujalle (0 = kuollut, 1 = elävä). Sekamallin vastemuuttujan jakauma oli yij ~ Bin(πij,1), ja yhden satunnaisparametrin (u) mukainen malli on:
![]()
jossa πij on vastemuuttujan odotusarvo puulle i metsikössä j ja uj edustaa metsikön j satunnaista poikkeamaa odotusarvosta jakauman u ~ N(0,su2) mukaisesti. Mallit sovitettiin SAS-ohjelmiston NLMixed-proseduurilla.
Vaihtoehtoisista malleista kaksi muotoiltiin ilman metsikön ikää siten, että läpimitan (d) neliön d2 avulla voitiin kuvata suurimpien kuusten pienenevää eloonjäämisen todennäköisyyttä (Yhtälöt 4 ja 5). Puiden välistä kilpailua kuvattiin kohdepuuta suurempien puiden pohjapinta-alalla (BAL). Muunnos BAL/√d osoittautui erittäin tehokkaaksi selittäjäksi. Harvennus oli malleissa mukana, koska eloonjäämisen todennäköisyys lisääntyi merkitsevästi 6–10 vuotta sitten tehdyillä harvennuksilla. Yhtälöissä 6–8 oli iän ja läpimitan yhdysvaikutus. Yhtälöissä 7 ja 8 oletettiin, että yhdysvaikutustermi b3d2 (Ikä/100) yhtälössä 6 saattoi olla liian voimakas, ja siksi haettiin optimaalisempia eksponentteja p1 ja p2. Eksponentit p1 ja p2 yhtälössä 7 olivat 1,8 ja 0,8 ja yhtälössä 8 ne olivat 1,4 ja 0,9, eli ne olivat pienempiä kuin yhtälön 6 vastaavat arvot 2 ja 1.
![]()
![]()
![]()
![]()
![]()
Sovitettujen yhtälöiden 4–8 tilastolliset yhteensopivuustestit (–2 log-likelihood, AIC, BIC) paranivat systemaattisesti yhtälöstä 4 yhtälöön 8. Mallien käyttäytymistä kuvattiin luonnontilaisen metsikön keskitunnuksilla (pohjapinta-ala 38 m2 ha–1, runkoluku 1010 ha–1, pohjapinta-alalla painotettu keskiläpimitta 30 cm), mutta vaihtelemalla metsikön keski-ikää 100 vuodesta 250 vuoteen. Yhtälön 8 käyttäytymisestä puun läpimitan (d) ja metsikön iän mukaan nähdään, kuinka metsikön ikääntyessä suuriläpimittaisen kuusen eloonjäämisen todennäköisyys (P) voimakkaasti pienenee (Kuva 1). Kun mallissa oli yhtäaikaisesti ikä ja yhdysvaikutustermi (Yhtälö 8), eloonjäämiskäyrät leikkasivat toisiaan pienemmissä läpimittaluokissa (Kuva 1).
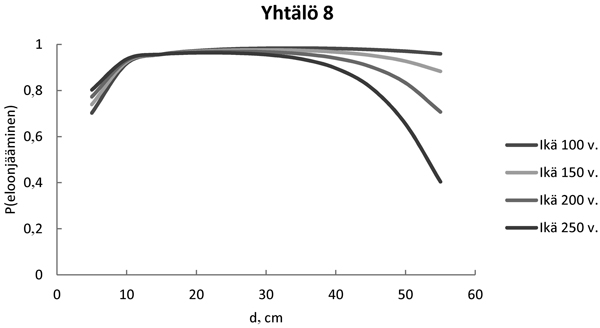
Jos malleissa ei ollut ikää (Yhtälöt 4 ja 5), niin mallit aliarvioivat eloonjäämistä hoidettujen metsien suurissa läpimittaluokissa ja puolestaan yliarvioivat sitä vanhoissa luonnonmetsissä laajalla läpimitan vaihtelualueella. Kun malleissa oli iän ja koon yhdysvaikutus, niin eloonjäämisennusteet olivat uskottavampia. Yhtälön 8 mukaisen eloonjäämismallin testitulokset olivat parhaat ja eloonjäämisen ennusteet sekä hoidetuissa metsiköissä (HARKAS) että luonnontilaisissa metsiköissä sopivat hyvin näihin aineistoihin. Kuvan 2 mukaiset tulokset tukivat hypoteesia, että puun ikä vaikuttaa puun eloonjäämiseen ja ikääntymisen liittäminen eloonjäämismalliin paransi selvästi eloonjäämisen ennusteita.
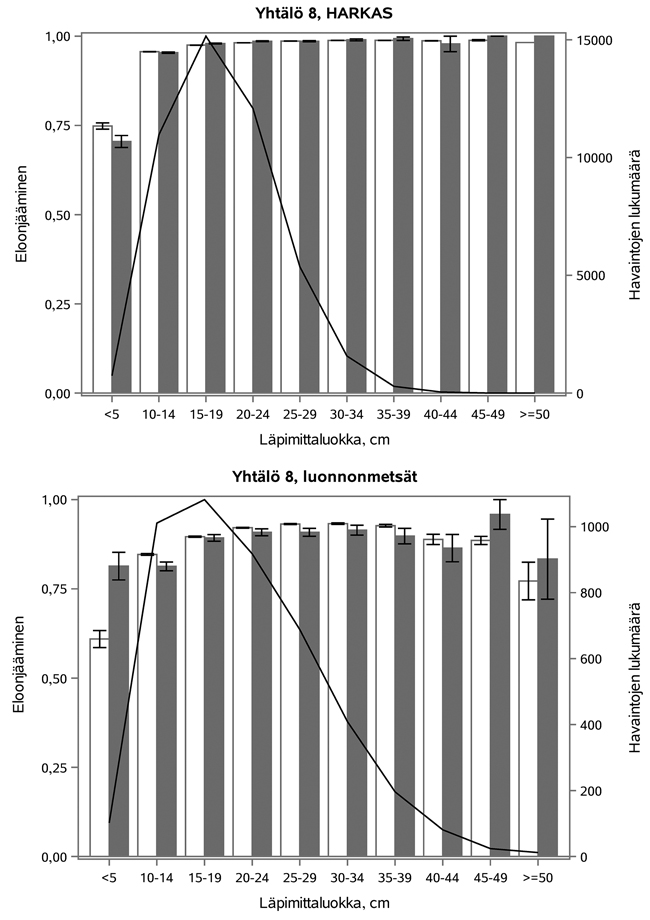
Kuva 2. Yhtälön 8 mukainen eloonjääminen hoidetuissa metsissä (HARKAS) ja luonnonmetsissä.