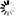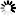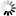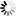Seloste artikkelista Lee D., Siipilehto J., Hynynen J. (2021). Models for diameter distribution and tree height in hybrid aspen plantations in southern Finland. Silva Fennica vol. 55 no. 5 article id 10612. https://doi.org/10.14214/sf.10612.

Hybridihaapa (Populus tremula L. × P. tremuloides Michx.) tunnetaan erittäin nopeasta kasvusta sekä hyvistä puuaineen ominaisuuksista. Siitä huolimatta malleja hybridihaavan kasvattamisen tueksi ei ole laadittu Pohjois-Euroopassa. Tutkimuksessamme esittelimme menetelmiä ja malleja hybridihaavikon läpimittajakauman ja puiden pituuden ennustamiseksi. Aineistona oli neljä toistuvasti mitattua (7–12 mittauskertaa vuodesta 1997 vuoteen 2016) istutetun hybridihaavan kenttä­koetta, jotka sijaitsivat Lohjan Jalassaaressa ja Kirkniemellä, Lapinjärvellä ja Pornaisissa. Kokeessa vertailtiin neljää eri viljelytiheyttä: 400, 800, 1200 ja 1600 tainta hehtaarilla. Koealoja, kooltaan 1000 m², oli 4–24 kpl kullakin koealueella, ja koealatason havaintoja oli kaikkiaan 294.

Läpimittajakauma ratkaistiin parametrin palautusmenetelmällä ja pituuden ennustamiseksi laadittiin kaksi mallia Näslundin pituuskäyrään perustuen. Kahden parametrin Weibull-jakauma voidaan ratkaista parametrin palautusmenetelmällä tietyn keskitunnuksen ja toisen momentin avulla. Toinen momentti on sama kuin neliökeskiarvon neliö (DQ²) ja se saadaan pohjapinta-alan (G) ja runkoluvun (N) avulla kaavalla DQ² = G/(N × q), jossa q on konversiokerroin π/200² = 7,854E−05. Tarkasteltuja keskitunnuksia olivat aritmeettinen keskiläpimitta (D), pohjapinta-alapainotteinen keskiläpimitta (DG), mediaani (DM) ja pohjapinta-alan mediaaniläpimitta (DGM). Palautetun jakauman yhteensopivuutta havaittuun jakaumaan tarkasteltiin Kolmogorov-Smirnov (KS) ja Error Index (EI) -testien avulla. Tulosten mukaan mediaani DM oli epäluotettavin keskitunnus ja yhteensopivuus hylättiin 34 % tapauksista (101 jakaumaa 294 jakaumasta). Kun käytettiin DGM-muuttujaa, hylkäyksiä oli 12,6 %, D-muuttujalla 5,1 % ja DG-muuttujalla vain 2,7 %. Esimerkit palautetuista jakaumista eri keskitunnuksilla kolmelle koealalle osoittavat suhteellisen pieniä eroja muiden keskitunnusten kuin mediaanin DM välillä (Kuva 1). Pahimmillaan palautettu jakauma oli niin huipukas, että kaikki puut kuuluivat mediaanin DM määrittämään läpimittaluokkaan.

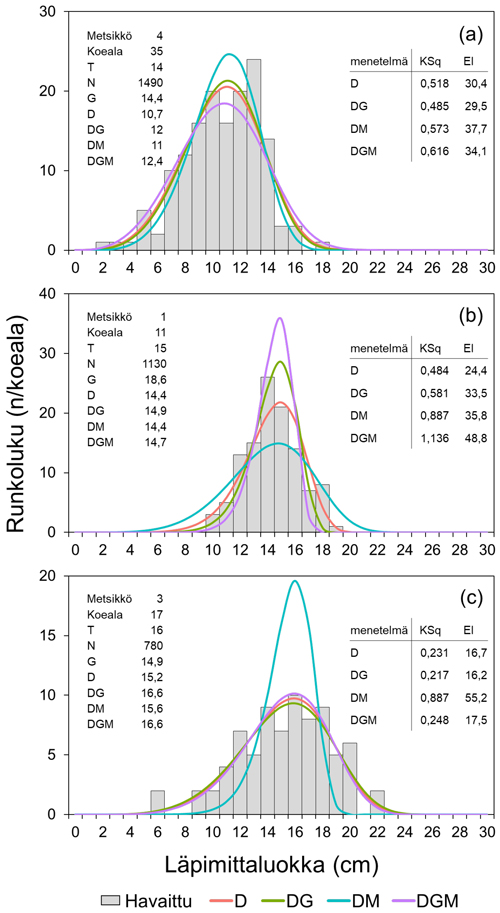
Kuva 1. Esimerkit kolmesta koealasta, joissa mediaani tuotti muista keskitunnuksista poikkeavan ratkaisun. Koealan puustotunnukset ovat kuvissa vasemmalla: T ikä, N runkoluku, G pohjapinta-ala, D keskiläpimitta, DG pohjapinta-alalla painotettu keskiläpimitta, DM mediaani ja DGM pohjapinta-alan mediaaniläpimitta ja jakaumien yhteensopivuudet oikealla: KSq Kolmogorovin-Smirnovin quotum ja EI Error Index. Harmaat pylväät kuvaavat havaittua jakaumaa ja KSq > 1 tarkoittaa yhteensopivuuden hylkäämistä Kolmogorovin-Smirnovin testillä 10 % riskillä. Esimerkissä a) kaikki ratkaisut olivat tilastollisesti yhteensopivia, mutta keskiarvot (D, DG) olivat mediaaneja (DM, DGM) parempia; b) mediaaneista DM tuotti liian laakean ja DGM liian huipukkaan jakauman ja c) DM tuotti huipukkaan ja huonosti yhteensopivan ratkaisun.

Estimoitu Näslundin käyrä pituudelle h läpimitan d funktiona oli muotoa h = (d/(exp(b₀) + exp(b₁) d))² + 1,3. Kun parametrit estimoidaan muodossa exp(b_i), niin ne saavat aina positii­visen arvon, mikä on edellytys järkevän pituuskäyrän muodolle. Lisäksi aikaisemmin on havaittu logaritmisten parametrien ln(b_i) voimakas lineaarinen riippuvuus keski- ja valtapituuden ln(HG) ja ln(Hdom) suhteen. Pituusmalli laadittiin epälineaarisena sekamallina sisältäen satunnaisen vakion ja satunnaisen kertoimen neljälle koealueelle. Mallin laadinnassa käytettiin R-ohjelmiston nlme-pakettia. Potenssifunktiolla huomioitiin jäännösvirheen heteroskedastisuus. Koska DG oli paras keskitunnus läpimittajakauman ratkaisemiseksi, se valittiin selittäväksi muuttujaksi pituusmalleihin. Muita pituuskäyrän selittäviä muuttujia olivat pohjapinta-alapainotteinen pituus (HG), ikä (T), G ja d (Malli 1). Lisäksi laadittiin Malli 2, jossa oli Mallin 1 selittäjien lisäksi runkoluku N. Malli 1 osoittautui herkäksi DG- ja HG-muuttujien muutoksille, kun taas Malli 2 oli herkkä puuston tiheyttä kuvaavien muuttujien G ja N muutoksille. Mallit olivat harhattomia puusto­tunnusten suhteen, mutta Malli 1 oli hieman harhainen puun suhteellisen koon d/DG suhteen, kun taas Malli 2 oli myös sen suhteen harhaton. Kuitenkin Mallia 1 voitiin pitää luotettavampana, koska pituuskäyrän ennusteet seurasivat tarkasti DG- ja HG-selittäjien muutoksia. Parametrien palautusmenetelmä DG-muuttujan avulla ja ennustetut Näslundin pituuskäyrät luovat vankan pohjan hybridihaavan läpimitan ja pituuden ennustamiseksi.

Lähteitä

Siipilehto J, Mehtätalo L (2013) Parameter recovery vs. parameter prediction for the Weibull distribution validated for Scots pine stands in Finland. Silva Fenn 47, article id 1057. https://doi.org/10.14214/sf.1057.

Siipilehto J, Kangas A (2015) Näslundin pituuskäyrä ja siihen perustuvia malleja läpimitan ja pituuden välisestä riippuvuudesta suomalaisissa talousmetsissä. Metsätieteen aikakauskirja, artikkelitunnus 6584. https://doi.org/10.14214/ma.6584.